4次元空間でプレイするテトリスとそれを自動プレイするAIの話
前に作ったゲームの解説的なお話です.
↓過去の記事
↓プレイ動画
はじめに
丁度2か月ほど前に,時間が空いていて,更にサークルで成果物発表会があったので,それに合わせてゲームを1つ作りました.
それが上の頭おかしい「4次元テトリス Tetris Dim.4」です.
DLはこちら↓
https://bitbucket.org/WGGSH/tetrisdim4/downloads/TetrisDim4_Ver0.60.zip
この記事は,4次元テトリスのルール解説と,AIの実装方法についての解説記事です.
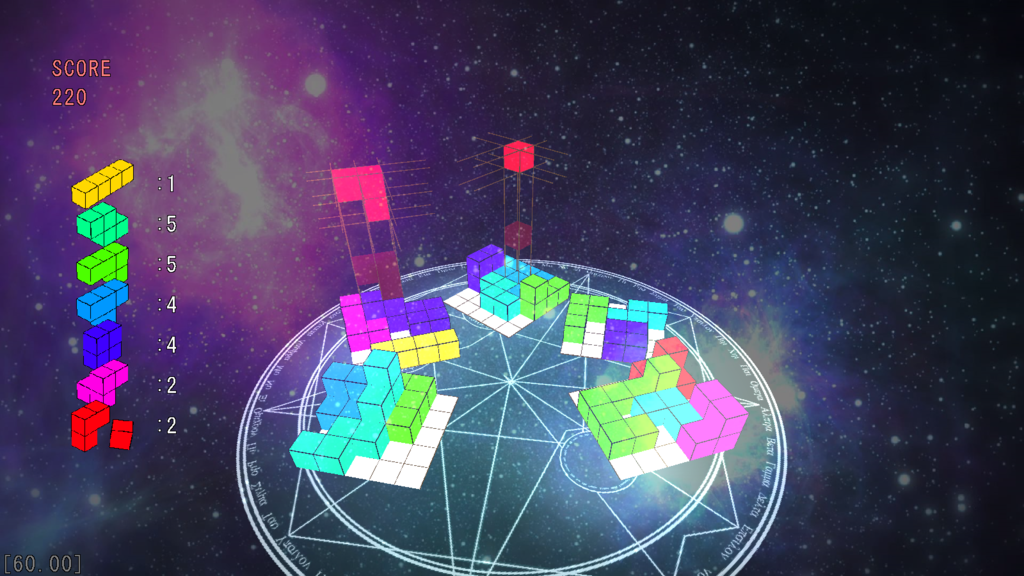
4次元テトリスのルール
一般的なテトリスは「10×20」のフィールドで,「7」種類のブロックを回転させて1列全て埋めてラインを消すことを目的とします.
4次元テトリスでは,上記ルールをそのまま次数を2つ上げただけです.
細かい数字まで言うと,
「5×5×5×10」のフィールドで,「7」種類のブロックを「6」つの回転軸で回転させて「5×5×5」の空間を埋めて消すことを目的とします.
次数と,移動方向・回転軸・ブロックの種類の対応表は以下の通りです.
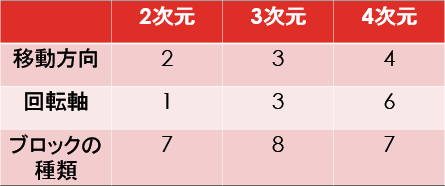
『なんで3次元の方が4次元よりブロックの種類が多いんだ?』
って疑問が出ると思います.
各次数のブロックを描いてみました
2次元

3次元
4次元(少し強引な可視化)
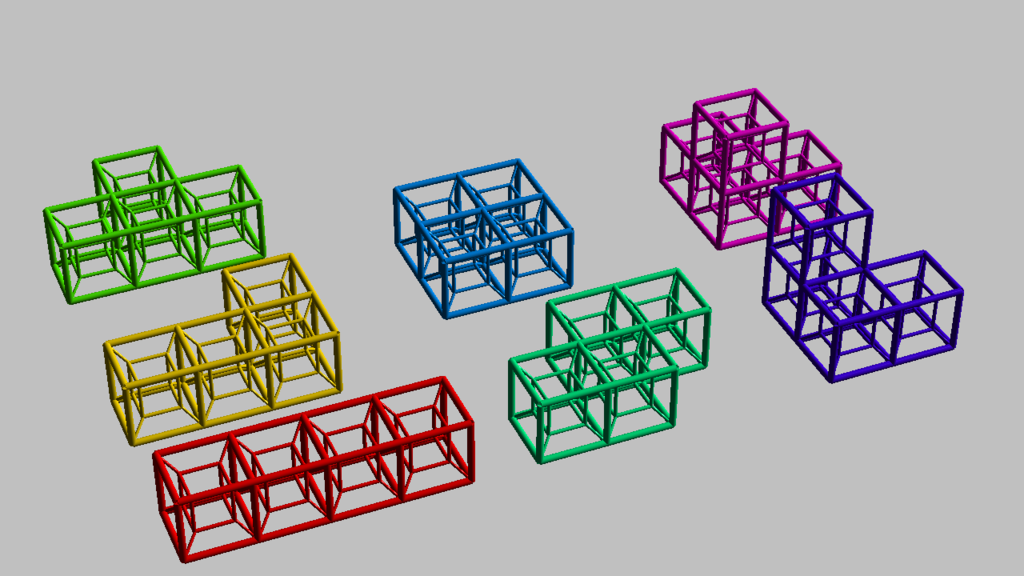
2→3次元
まず,2次元から3次元でブロックが1つ増える点についてみて見ます


上の画像に描かれている3つのブロックは2次元空間では表現できない為,3つ増えます
ところが下の画像ではそれぞれ2次元で2種類だったブロックが3次元になることで1つに統一できます.これは回転軸が増えたためです.
3個の増加と,2この減少,結果的に1つ増えて8種類になります.
3→4次元
では,3次元から4次元ではどうなるのでしょうか.

3次元から4次元になっても,新しい形のブロックパターンが増えることはありません.何故なら,4次元でしか表現できないパターンを作るには,ある1マスから別々の4つの軸の方向へ隣接するブロックが存在する必要があります.2次元から3次元にした時は,これが存在しましたが,3次元から4次元では存在しません.そもそも1つのパターンを構成するブロックの数が4なので,4方向に伸ばすためには構成するブロックが最低5つ必要になります.
対して,3次元で存在していた2つのパターンが4次元で増えた回転によって,同一視できるようになります.
結果,3次元と比べて,1つパターンが減り,合計7種類になります.
回転
上の表では4次元の場合,回転軸が6つと書いていました.
任意の次元数 n次元空間において,2つの軸からなる平面で回転する回転軸は(n-2)!個です.
有名なアレ
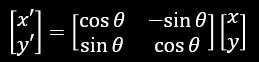
数学の教科書にも出てくるアレです(2次元版)
4次元では↓の様になります.この中で,sin,cosを使用する軸を2つ選ぶのですが,その組み合わせが6通り存在します.
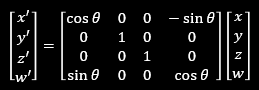
という訳で,ここまでで一応4次元の動きについて軽く説明が終わりました(疲れた
こっからAI
さて,ここからAIの実装についてです.
といっても,適当にネットから参考になりそうな記事を拾ってきて4次元テトリスに対応させた程度の事しかしていないのですが...
↓参考にした記事たち
GitHub - takuma7/tetris-ai-generator: This program is to seek strong tetris AI with the power of GA
AIの基本的な考え方
今回作成したAIは「評価関数」を用いています
計算手順は以下の感じです
- ブロックを置くことができる場所を全て探す
- 1で見つけた場所全てに対して,ブロックを置いた後の状態を複数の観点から評価する
- 最も評価の合計点が高い場所が,「置くべき場所」
まぁ凄く単純です.単純ですが4次元にしたことでいくつか問題が浮上しました.
1.ブロックを置くことができる場所を全て探す
コンピュータの計算速度を利用して,全てのパターンをシミュレートします.
そのためには何パターン置くことができるか調べなくてはいけません.
ブロックの置く場所は「移動量」「回転角度」で決定します.
移動量は非常にシンプルです.フィールドサイズが「5×5×5×10」で,10は落下にあたるので,それ以外の「5×5×5」=125通りが上限です.当然,ブロックの形によってこれより少なくなることもあります.
ところが回転は,回転軸が6つと書いたのですが,回転順序が関わってきます.
例として,6つの回転軸をA~Fとすると,Aで90°→Bで90°回した形と,Bで90°→Aで90°回した形は同じになるとは限りません.これは行列の積が順番を変えると結果が変わるのと同じですね.
全ての回転後の姿勢を求めるには,(書く回転軸の角度パターン)^(回転軸の個数)×(回転順序の組み合わせ総数)で求められます.
つまり, (4の6乗)×(6の階乗)=2,949,120通りです(絶望
これに移動量の上限125を掛けるので......1手ごとにシミュレートすべきパターン総数は
368,640,000 通り(最大)
になります。無理です.計算しきれませんでした()
という訳で,大幅な妥協をすることにしました.
移動を妥協したら特定のマスにブロック置けなくなるので,こっちはスルーで,回転パターンを大幅に制限しました.
「6つの回転軸を好きな順番で回す」→「ある決められた3つの回転軸を指定した順番で回す」へと変更しました.
4次元のパズルが活かせていないかもしれませんが...やむを得ずそうしました.
これで2,949,120通り存在した回転パターンは64通りまで減りました(少なっ
移動と合わせても合計で,最大8,000パターンです
2.1で見つけた場所全てに対して,ブロックを置いた後の状態を複数の観点から評価する
ここが「評価」にあたる部分です.1で8000種類置くべき場所を見つけたので,それら全てを以下の判断基準から評価していきます.
- 最もブロックで埋まっている段のブロックの数
- 消した段の数
- Z(落下)座標が上から4マス以内に存在するブロックの数
- ホールの数
- 落下位置のZ座標
- 最大高度
まあこのぐらいにしました.これらに対して,「重み」をつけることで,AIの性格を表現することができるようになります.
1つずつ説明していきます.
1.最もブロックで埋まっている段のブロックの数
4次元テトリスでは1段消すのに125個のブロックが必要です(2次元なら10個)
これを効率よく積んでいくために,最もブロックで埋まっている段を調べて,その数を評価値にします.ブロックを平らに積んで,消すスピードが向上すると考えられます.
2.消した段の数
言うまでもないですね.ブロックを消すことがこのゲームのメインなので.
ここを,4段消せるとき以外は評価を低めに設定したりすると,4段消し(テトリス)を決めやすいAIをつくったりすることができます.
3.Z(落下)座標が上かrあ4マス以内に存在するブロックの数
これは少しわかりづらいですが,ブロックを高く積みすぎると,移動可能な領域が減り,難易度が大幅に向上します.そのため,ある程度高く積むことに対して,負の重みをつけることで可能な限り回避します.
4.ホールの数
ブロックの下に空いているマスがあると,その段を消すためには上の段を消さなければいけません.2次元なら10個のブロックで消すことができますが,この4次元テトリスでは125個必要で,非常に負担がかかります.正直言うと一度ホールをつくったら,それを修復するのはほぼ不可能です.そこで,ホールを作ることに対して負の重みをつけて,回避します.
5.落下位置のZ座標
1と3があるのでこれは無くてもよかったかもしれません.より平らに積んでもらうために,低いところに置くと評価が高くなるようにしています.
6.最大高度
同じく,不要だったかもしれません.これも平らに積むための評価基準です.
これらの評価を用いて,「最も評価の高い移動場所」を決定します.
3.最も評価の合計点が高い場所が,「置くべき場所」
あとは簡単です.2で決めた場所に対してブロックを移動させるだけです.
おわり
以上,4次元テトリスのルールとAIの作成方法についてのメモ兼説明でした.
良かったらプレイしてみてくださいね
DLリンク↓
https://bitbucket.org/WGGSH/tetrisdim4/downloads/TetrisDim4_Ver0.60.zip
